Was ist der Sinn der Mathematik? Was überhaupt ist Mathematik? Warum braucht “man” sie? Warum braucht man sie nicht? Wo sind ihre Grenzen? Wo ihre Stärken? Was lehrt uns der Vergleich von Natur und Mathematik? Und warum muss sich unsere Einstellung zum Sinn der Mathematik ändern?
Genug 8en, Genug 9, Genug 4en, Genug 5en
27, 8 Milliarden, 3 Millionen, Trilliarden
Gleich, gleich, Hoch, hoch …
Das gelobte Land der Mathematik – Die Radierer
Was ist Mathematik?
Definition
Die Mathematik aus dem Altgriechischen μαθηματική τέχνη (mathēmatikē téchnē) = die Kunst des Lernens ist eine Formalwissenschaft. Geschichtlich enstand sie aus der Untersuchung von geometrischen Figuren einerseits und dem Rechnen mit Zahlen andererseits. Es gibt für den Begriff Mathematik keine allgemein anerkannte Definition. Üblich ist es heute, sie als eine Wissenschaft zu beschreiben, die durch logische Definitionen selbstgeschaffene abstrakte Strukturen mittels der Logik auf ihre Eigenschaften und Muster untersucht.
(Meine) Erfahrungen mit Mathematik
Studium
Ich bin selbst kein unbeschriebenes Blatt, was Mathematik angeht. So durfte ich durch mein Studium tiefe Einblicke in die Mathematik genießen. Darüber hinaus kenne ich die Bedeutung dieser sehr grundlegenden Wissenschaft für alle Naturwissenschaften und allen voran für die Physik. (Randbemerkung: Die Physik wiederum untersucht grundlegende Phänomene der Natur und des Universums, beschäftigt sich aber explizit nicht mit der lebenden Materie.).
Betreibt man Mathematik als Wissenschaft, so führt man viele Beweise. Leitet Sätze und Lemmata aus Axiomen und Definitionen ab, rein durch Logik. Durch solche logischen Gedankengänge und Beweisführungen (etwa den Beweis durch Widerspruch u.a.) kommt man in der Mathematik sehr schnell auf Symmetrien und Strukturen, deren Eigenschaften und Muster man wie gesagt untersuchen kann.
Algebra
Was sicherlich jeder aus der Schule kennt, sind Zahlen-Körper, in denen zu Rechnen an sich schon viele Schülerjahre und sicher auch so manchen Schüler-Albtraum ausfüllt. Auch Zahlen selbst haben eine Struktur, deren algebraische (ich würde kurz sagen: “zahlerische”) Krönung dieser kurze Satz ist:
Die komplexen Zahlen sind algebraisch abgeschlossen.
Fundamentalsatz der Algebra
Er besagt (etwas flachsig) letztlich, dass man durch Rechnungen nicht aus dem Körper der komplexen Zahlen hinaus kommt. Er ist sogesehen “abgeschlossen”.
Auch die sogenannten “algebraischen Zahlen” (Nullstellen von Polynomen mit ganzzahligen Koeffizienten) strukturieren die komplexe Ebene:
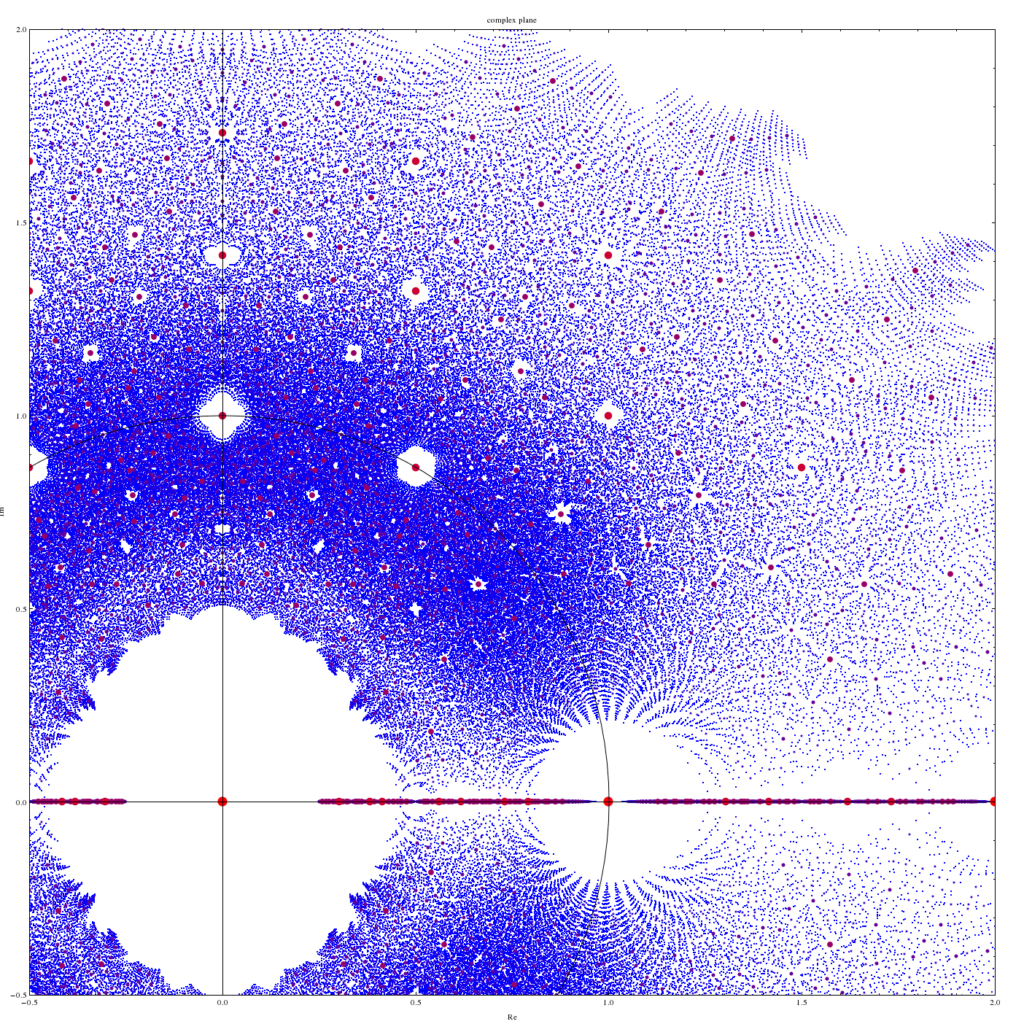
Funktionentheorie
Zusammen mit den transzendenten Zahlen “e”, der Eulerschen Zahl, und “π”, der Kreiszahl, sowie der komplexen Zahl “i”, dem neutralen Element der Addition “0” und schließlich dem der Multiplikation “1” ergibt sich eine tiefe Wahrheit in der Mathematik der Funktionentheorie, die Eulersche Identität:
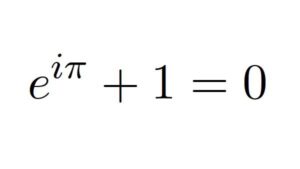
Logik – der tiefere Sinn der Mathematik
Logik ist enorm wichtig in der Mathematik. Ohne sie wäre Mathematik willkürlich und chaotisch zugleich. Mit ihr aber leiten sich aus der Mathematik tiefe Wahrheiten ab.
Vom Wortstamm gesehen kommt Logik vom altgriechischen Ausdruck logos (λόγος (lógos)). Dieser Ausdruck ist nicht einfach ein Wort. Eine ganze Erkenntniswelt verbirgt sich hinter “logos”.
Auf der einen Seite wird es unspezifisch im Sinne von „Wort“ und „Rede“ sowie deren Gehalt („Sinn“) gebraucht, auf der anderen Seite bezeichnet es aber auch das geistige Vermögen und was dieses hervorbringt (wie „Vernunft“). Es kann auch ein allgemeineres Prinzip einer Weltvernunft oder eines Gesamtsinns der Wirklichkeit meinen. Und damit nicht genug. Auch spezifischere Verwendungen, beispielsweise als „Definition“, „Argument“, „Rechnung“ oder „Lehrsatz“ existieren je nach Kontext.
“A ⇒ B” ⇔ “¬B ⇒ ¬A”
Zusammen mit der Sprache bildet die Logik den Grundstein menschlichen Denkens. Die Sprache wiederum ist natürlich einerseits regional geprägt, wie Ungarisch, Englisch, Japanisch, Deutsch und vieles mehr. Andererseits gibt es aber viele Worte und Strukturen in der menschlichen Sprache, die auf eine gemeinsame, irdische “Ursprache” aller Menschen deuten. Für je zwei Sprachen gibt es mindestens einen Menschen, der beide Sprachen spricht.
Warum Mathematik?
Ohne Logik ist menschliches Denken in gewisser Weise willkürlich. Es reduziert sich auf Meinungen, Gefühle und Befindlichkeiten oder bestenfalls nackte Information oder Fakten. Erst mit der Logik formt sich der menschliche Verstand. Kommt der Mensch zur Ratio, zur Vernunft. Und nur so kann er echtes Wissen erlangen.

Mit der Vernunft kann er philosophieren und durch seine philosophischen Gedanken zu Weisheit und Wahrheit gelangen. Da niemand die Wahrheit für sich beanspruchen kann, ist der Diskurs zwischen Menschen elementar. Eine Meinung trifft auf eine andere, eine Behauptung auf eine Gegenbehauptung.
A oder ¬A
Die Diskussion, das Gespräch untereinander, entbehrt ganz ohne Logik eines elementaren Grundbausteins. Dennoch sollte man klar sehen, dass es weitere solcher Grundbausteine gibt, wie etwa Sprache, Wahrnehmung, Liebe oder Vertrauen. Jeder wird mit diesen Begriffen etwas konkretes verbinden. Mir ist hier wichtig, dass sie das menschliche Denken und Fühlen mit der Logik zusammen elementar beeinflussen.
Mathematik schafft Strukturen durch Logik. Sie liefert also rationale, vernünftige Sicherheit. Mathematik strukturiert. Strukturiert das Denken selbst. Sie schafft logische Folgerungen, ohne diese jedesmal neu aus den Voraussetzungen ableiten zu müssen.
Ich habe mal gehört, dass vor allem unsichere Menschen eine Vorliebe für Mathematik haben. Vielleicht um sich daran fest zu halten? Den Verstand zu klammern? Sinn der Mathematik als Sicherheitssinn?
Grenzen und Stärken
Werkzeuge durch Mathematik
Ohne Mathematik bleibt dem Menschen ein Großteil der Struktur unserer Welt und des Universums verborgen. Im Zusammenspiel mit den Naturwissenschaften aber schafft es die Mathematik, Unbekanntes zu verstehen und zu entdecken, Zusammenhänge herzustellen und sogar Dinge beherrschbar zu machen. Hieraus ergibt sich direkt ein Sinn der Mathematik.
Eine Maschine ist ohne Mathematik nicht denkbar. Eine gesteuerte Bombe ebensowenig. Letztere würde rein zufällig explodieren. So kommt es, dass Mathematik auch viel mit Macht zu tun hat. Sie liefert Werkzeuge, um Dinge und letztlich auch Menschen zu beherrschen.

Die friedliche, positive Stärke der Mathematik ist vor allem der Erkenntnisgewinn. Die letztlich durch Mathematik als vernünftiger Wissenschaft geschaffenen „Werkzeuge um zu beherrschen“ lassen sich sowohl positiv als auch negativ nutzen. So wie das Verständnis des Feuers Wärme oder Zerstörung bringen kann, kann dies auch eine schlichte mathematische Information oder Wahrheit.
Mathematik ohne Fehler?
Eine weitere wichtige Grenze der Mathematik ist nach meiner Erkenntnis, dass Mathematik stets auf Fehlerfreiheit aufbaut. Ja, richtig gelesen. Genau diese Fehlerfreiheit nämlich ist ein Makel der Mathematik. Ich finde vielmehr, dass erst im Zusammenspiel mit dem Fehler die Mathematik ihre wahre Kraft entfaltet.
Eine fehlerfrei hergeleitete, mathematische Theorie ist wunderschön. Dennoch ist sie fast sinnfrei, wenn sie sich nicht auf die fehlerhafte Realität anwenden lässt. Jeder noch so kleine Sachverhalt im Universum ist mit Fehlern behaftet. So kommt es, dass man ein rein mathematisches Ergebnis nicht ohne weiteres übertragen kann. Man muss sich zwangsläufig Gedanken um mögliche Fehler machen.
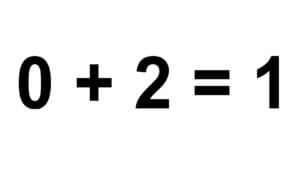
Ein einfaches Beispiel ist der mathematische Kreis, den es in der Wirklichkeit nicht gibt. Auf einem realen „Kreis“ haben zwei Punkte immer einen geringfügig anderen Abstand vom Mittelpunkt, und nicht den exakt selben wie in der mathematischen Definition des Kreises. Das mag spitzfindig klingen, ist aber eine wichtige Erkenntnis.
Ausnahmen bestätigen die Regel: Eine besondere Sinnstiftung aus Mathematik
Dennoch fällt mir sogleich ein wichtiges Beispiel ein, wo Mathematik sehr wohl die Fehlerhaftigkeit mit einbezieht. Sie wird dort besonders philosophisch. Es ist ein Beispiel aus der Quantenphysik: die Unschärferelation.
Die Herleitung ist erstaunlich einfach. Ich will sie deshalb kurz skizzieren:
Seien A und B zwei physikalische Größen, deren Operatoren A* und B* nicht kommutieren, d.h.
[A*, B*] = A*B* – B*A* ≠ 0
Dann folgt durch sehr einfache Rechnung in sog. Bra-Ket-Schreibweise (man braucht nicht viel Mathematik), dass
ΔA * ΔB ≥ 1/2 <phi| [A*, B*] |phi> ≠ 0
Wobei ΔA und ΔB jeweils die
- Quantenfluktuationen,
- Varianzen der zu A und B gehörigen Operatoren,
- Ungenauigkeiten oder auch
- Unschärfen
sein können.
Hier hat man also ein weitreichendes physikalisches Grundprinzip mit sehr wenig Mathematik hergeleitet bzw. aus wenigen Grundannahmen bewiesen. Es besagt, dass man zwei komplementäre physikalische Größen niemals gleichzeitig beliebig genau messen kann. Ja sogar, dass ihr grundsätzlicher Fehler bei der Messung endlich groß ist.
Anwendung der Unschärferelation
Für meine Begriffe am bahnbrechendsten ist diese Erkenntnis für die beiden komplementären Größen Energie und Zeit, deren Kommutator ungleich Null ist. Das hat nämlich unmittelbare Auswirkungen auf den Urknall. Geht man zeitlich nur nahe genug an diesen scharfen Zeitpunkt auf dem Zeitstrahl heran, so wird, da die Zeit sehr genau ist, die Energie sehr ungenau: es werden riesige Energiemengen frei.

Ein Universum entsteht.
Umgekehrt folgen für sehr kleine Energiemengen (wie etwa in einem winzigen Samenkorn) sehr große Zeiträume (Zeitunschärfen). So könnte also ein sehr kleines Samenkorn sehr lange seine sehr kleine geringe Energie halten.
Natur und Mathematik

Es hilft nichts, wunderschöne Strukturen, Symmetrien zu erkennen, wenn man nicht auch die Möglichkeit des Fehlers hinzu nimmt. Durch einen Fehler entsteht Neues. Ein Fehler kreiert eine Abweichung. Im Extremfall eine Abweichung von Nichts. Also Etwas.
Mathematik kann nur auf etwas aufbauen. Weiterführen oder folgern aus etwas, was schon ist. Der Fehler aber ist etwas komplett Neues. Eine Kreation. Etwas Entstandenes. Entstandenen aus sonst immer gleich Bleibendem.
Letztlich ist es das Zusammenspiel von Determinismus und Chaos, von Vorherbestimmung und Zufall. Beide sind ohne einander nicht denkbar. Sie gehören zwangsläufig zum menschlichen Denken. Mehr noch. Sie sind Grundprinzipien unserer Welt. Unseres Universums.
Philosophisch landet man schnell bei Ying und Yang. Aber ich will nicht zu weit ausholen. Um bei der Mathematik zu bleiben: Die Mathematik kommt in der Theorie ohne Fehler aus. Aber ohne Fehler ist Mathematik für unsere Welt ein Irrweg, eine Täuschung. Perfektion mag ein Ziel sein, aber nichts, was tatsächlich erreichbar ist. Alles im Universum hat Fehler. Ohne zusätzliche Fehler an einem betrachteten System ergibt sich kaum eine sinnhafte Anwendung der Mathematik.

Der Kern der Natur ist ihre Fehlerhaftigkeit und zugleich ihre Verletzbarkeit. Jedes Leben ist vergänglich. Lässt sich nicht abbilden durch ewig währende Mathematik.
Fazit: Sinn der Mathematik aus heutiger Sicht
Aus heutiger Sicht ist es meiner Ansicht nach höchste Zeit für ein Umdenken.
Globale Herausforderungen wie der menschengemachte Klimawandel, die Ausbeutung von Mensch, Tier, Pflanze und Natur allgemein, das ewige Wettrüsten, die kurzsichtige Ausschlachtung irdischer Ressourcen auf Kosten der Grundlage höher entwickelten Lebens – dies alles sind Beispiele, die den Menschen zum Umdenken zwingen oder zumindest zwingen sollten.

Es darf nicht läger ausschließlich darum gehen, zu produzieren, zu optimieren, zu kontrollieren, zu beherrschen. Vielleicht darf es sogar gar nicht mehr darum gehen?
Es ist höchste Zeit für Rücksicht. Rücksicht auf die Natur. Rücksicht auf den Menschen. Der Mensch muss die Natur dringend als Verbündeten begreifen, gerade wegen ihrer Fehlerhaftigkeit.
Nur mit dem natürlichen Fehler gemeinsam hat die Mathematik, die rationale Wissenschaft, die Produktion und die Wirtschaft noch eine Daseinsberechtigung. Ohne Natur wird sie uns aber geradewegs ins Verderben, in den irdischen Untergang führen.
Gestalterisch versuche ich diese Erkenntnis u.a. in meiner Kunst, in der sogenannten “Spektralmathematik” zu verarbeiten. Beispiele dazu hier.
❤️
Hast Du nur ein Wort zu sagen, nur ein Gedanke dann
lass es Liebe sein.
Rosenstolz
… nicht “wahr” oder “falsch” – wie in der Mathematik – sondern “Liebe”!
SH, 05.2021

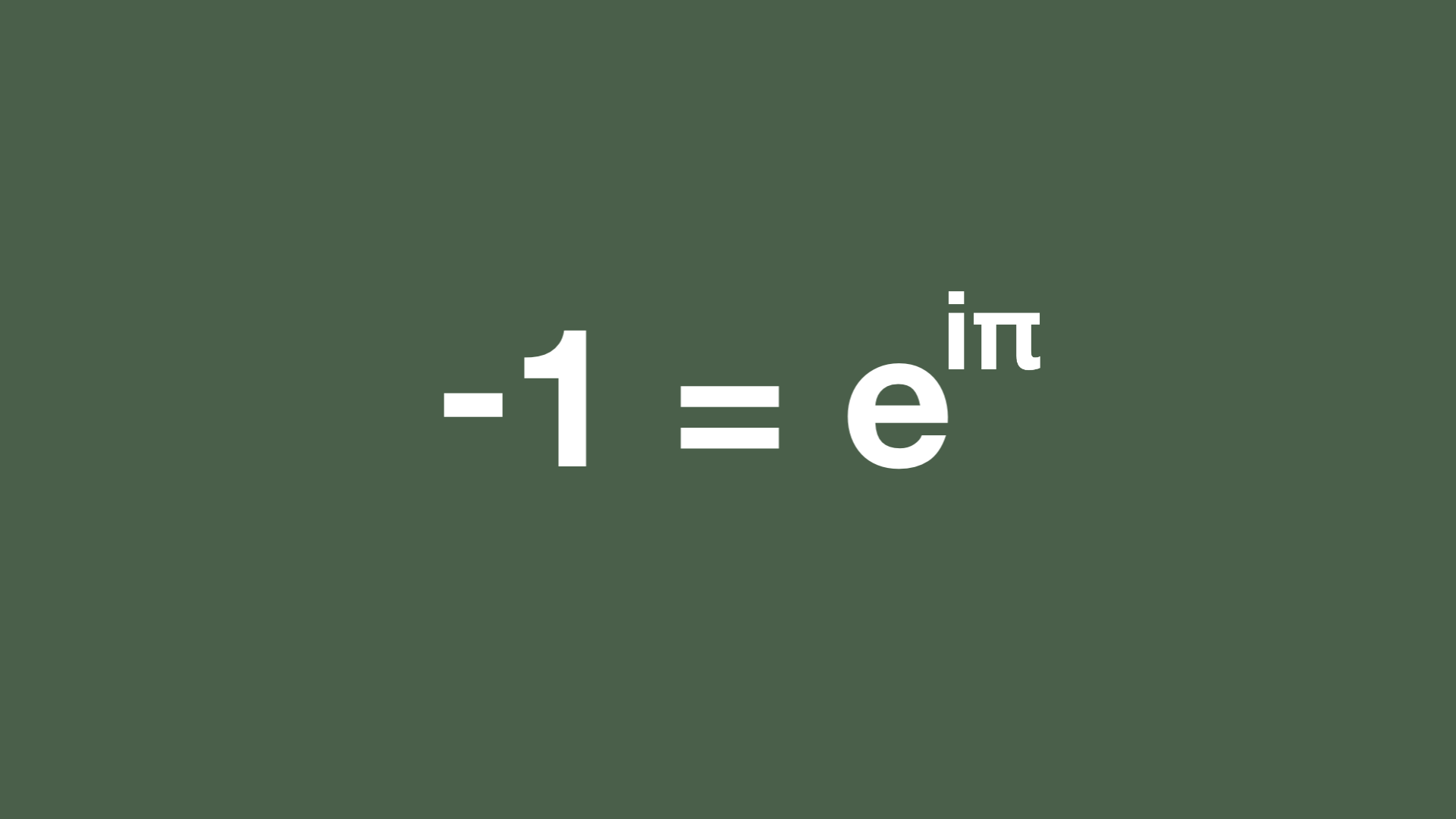
Schreibe einen Kommentar